Sample Code Generating String Combinations of Characters

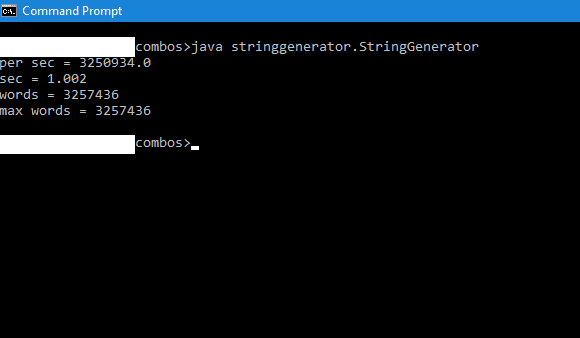
In my post here, I shared an algorithm to generate all possible combinations of a given set of characters for a specified range of lengths. In this post, I shall share a code sample written in Java that implements the algorithm shared before. It does not use any goto keyword and hence does not create sphagetti code.

The code uses the concurrency API of Java and is fully parallelized. It maxes out the CPU cores of a multi-core CPU and achieves a few million iterations per second. The code sample uses a custom utility function ‘power’ for calculating powers of integers. It is made static for more execution speed.
The code is commented in places to help readers understand it.

As with the algorithm, I take no responsibility for what is done with this code.

package stringgenerator;

import java.util.concurrent.*;
import java.util.concurrent.atomic.*;

public class StringGenerator implements Runnable
{
  private static char[] dict = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l'};  //allowed characters
  
  private static ExecutorService ex;
  
  private static AtomicLong attempts = new AtomicLong(0); //count the number of combinations generated
  
  private static Object locker = new Object();
  
  private static long maxAttempts = 0; //total possible combinations of characters of specified lengths
  
  private static int maxLen = 0;
  
  private static long getMaxAttempts(int radix, int maxLen)
  {
    maxAttempts = (power(radix, maxLen) - 1)*radix /(radix-1);
    
    return maxAttempts;
  }
  
  //utility function to calculate powers of integers
  private static long power(int base, int exp)
  {
    if(exp < 0)
    {
      return 1/power(base, -exp);
    }
    else if(exp == 0)
    {
      return 1;
    }
    else{
      long pow = 1;
      for(int p = 1; p <= exp; p++)
      {
        pow*=base;
      }
      
      return pow;
    }
  }
  
  //the main work horse of this program, breaking all possible numbers into combinations
  private static void resolveRadix(int len, long num)
  {
    long[] retVal = new long[len];
    
    int pow = 0;
    int i = -1;

    int radix = len;
    
    for(i = 0; power(radix ,i ) <= num; i++ );
    
    for(int j = 0; j < len - i; j++)
    {
      retVal[j] = 0;
    }
    
    for(int k = len - i; k < len; k++)
    {
      long t = power(radix, i - 1);
      if(i > 1)
      {
      
        retVal[k] = (long)((num - (num % t)) / t);
      
      }
      else
      {
        retVal[k] = (num % radix);
      }
      num -= (retVal[k] * t);
      
      i--;
    }
    
    char[] combo = new char[len];
    
    for(int j = 0; j < len; j++)
    {
      combo[j] = dict[(int)retVal[j]];
    }
    
    String str = new String(combo);
    
    final long attemptsVal = attempts.incrementAndGet();
    
    attempts.set(attemptsVal);
  }
  
  private void generate()
  {
    for(int length = 1; length <= maxLen; length++)
    {
      int radix = dict.length;
      
      long max = (long)power(radix, length);

      for(int i=0;i<max;i++)
      {
        resolveRadix(radix, i);
      }
    }
    
  }
  
  public void run()
  {
    generate();
    
    synchronized(locker)
    {
      locker.notify();
    }
      
    ex.shutdownNow();
    
  }
  
  public static void main(String[] args)
  {
    
    ex = Executors.newSingleThreadExecutor();
    
    maxLen = 6;
    
    long atts = getMaxAttempts(dict.length, maxLen);
    
    StringGenerator threads = new StringGenerator();
    
    long start = System.currentTimeMillis();  //execution start time
    
    ex.execute(threads); //execute code parallelly
    
    try{
        
      synchronized(locker)
      {
        locker.wait();
      }
    }
    catch(InterruptedException ie)
    {
      ie.printStackTrace();
    }
    
    long attemptsVal = attempts.get(); //final total number of attempts
    
    long end = System.currentTimeMillis(); //execution end time
    
    double speed = (double)((1000 * attemptsVal)/(end - start)); //rate of generating combos
    
    double seconds = (double)(end - start) / 1000;
    
    System.out.println("per sec = "+speed);
    
    System.out.println("sec = "+seconds);
    
    System.out.println("words = "+attemptsVal);
    
    System.out.println("max words = "+atts);
    
  }
}

Execution after compilation is shown below: