Tag: algorithms

How to generate combinations from a set of characters

In this post, I shall share a code sample in Java that generates string combinations of characters from a given set of characters over a specified range of lengths of such string combinations. I hope I am not boring you all with this topic,since it’s my third such code sample to this effect. The other two samples can be found here and here.

Note that this is my fastest such code yet. It maxes out the cores of a multi-core CPU on execution. Also note that I have no systematic algorithm for this one! Does that sound weird?

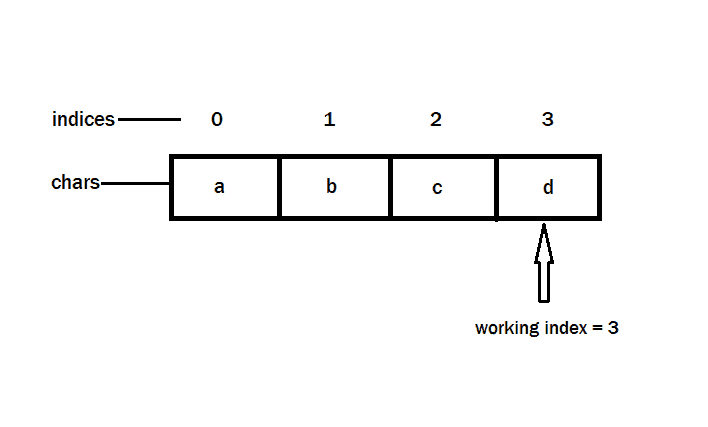
There is no exponentiation involved in this sample as in the one here. We simply map elements in an integer array to characters in a character array and then convert that character array to a string when we want to do something with it.

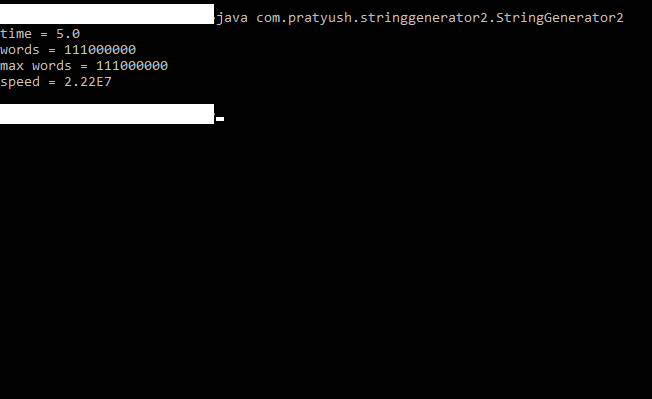
We manipulate indices in the integer array by incrementation and decrementation, that’s it. The code uses the concurrency APIs of Java and is fully parallelized. It achieved about twenty two million iterations per second during my tests.

Finally, let me say further that I take no responsibility for what is done with this code.

package com.pratyush.stringgenerator2;

import java.util.concurrent.*;

class StringGenerator2 implements Runnable
{
    private static char[] dictionary = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j'};
  
    static Object locker;
  
    static  ExecutorService es;
  
    static int attempts = 0;
  
    private static String getStringFromIndices(int[] indices, char[] str)
    {
    
      for(int z = 0; z < str.length; z++)
      {
          str[z]=dictionary[indices[z]];
      }
    
      return new String(str);
    
    }
  
    private static long getMaxAttempts(int startLen, int stopLen)
    {
        long myMaxAttempts = 0;
    
        for(int c = startLen; c <= stopLen; c++)
        {
            myMaxAttempts += Math.pow(dictionary.length, c); 
        }
    
        return myMaxAttempts;
    }

    public void run()
    {
    
       long start = System.currentTimeMillis();
    
       generate(6, 8); 
    
       long end = System.currentTimeMillis();
    
       double secs = (end - start)/1000;
    
       System.out.println("time = "+secs);
    
       System.out.println("words = "+attempts);
    
       System.out.println("max words = "+ getMaxAttempts(6,8));
    
       double speed = attempts / secs;
    
       System.out.println("speed = "+speed);
    
       synchronized(locker)
       {
        
           es.shutdownNow();
        
           locker.notify();
       }
    
   }
  
   public static void generate(int startLen, int stopLen)
   {
     int LEN = dictionary.length;
    
     attempts = 0;
    
     String strCombo = "";
    
     for(int currLen = startLen; currLen<= stopLen; currLen++)
     {
         char[] str = new char[currLen];
      
         int[] indexes = new int[currLen];
      
         for(int f = 0; f < indexes.length; f++) 
         {
             indexes[f] = 0;
         }
      
         for(int j = 0; j < LEN; j++ )
         {
             indexes[0] = j;
        
             if(currLen == 1)
             {
          
                 strCombo = getStringFromIndices(indexes, str);
          
                 /***generate string here and do whatever you like***/
          
                 attempts++;
             }
             else
             {
                 while(indexes[1]<LEN)
                 {
                     int i = 1;
            
                     for(i = 1; i < currLen; i++)
                     {
                        if(indexes[i] == LEN)
                        {
                            break;
                        }
              
                        if(i == currLen - 1)
                        {
                
                            strCombo = getStringFromIndices(indexes, str);
                                
                            /***generate string here and do whatever you like***/
                                
                             indexes[i]++;
                             attempts++;
                         }
                     }
            
            
                    for(int k = 2;k<currLen;k++)
                    {
                        if(indexes[k] == LEN)
                        {
                            indexes[k-1]++;
                                
                            for(int l = k; l<currLen; l++)
                            {
                                indexes[l] = 0;
                            }
                        }
                    }
                }
          
                for(int m = 1; m < currLen; m++)
                {
                    indexes[m] = 0;
                }
             }
          }
       }
    
    }
  
    public static void main(String[] args)
    {
    
      es = Executors.newSingleThreadExecutor();
    
      locker = new Object();
    
      es.execute(new StringGenerator2());
    
      try{
         synchronized(locker)
         {
            locker.wait();
         }
      }
      catch(InterruptedException ie)
      {
   ie.printStackTrace();
      }
    
   }	
}

 

Code execution after compilation is shown below:

Sample Code Generating String Combinations of Characters

In my post here, I shared an algorithm to generate all possible combinations of a given set of characters for a specified range of lengths. In this post, I shall share a code sample written in Java that implements the algorithm shared before. It does not use any goto keyword and hence does not create sphagetti code.

The code uses the concurrency API of Java and is fully parallelized. It maxes out the CPU cores of a multi-core CPU and achieves a few million iterations per second. The code sample uses a custom utility function ‘power’ for calculating powers of integers. It is made static for more execution speed.
The code is commented in places to help readers understand it.

As with the algorithm, I take no responsibility for what is done with this code.

package stringgenerator;

import java.util.concurrent.*;
import java.util.concurrent.atomic.*;

public class StringGenerator implements Runnable
{
  private static char[] dict = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l'};  //allowed characters
  
  private static ExecutorService ex;
  
  private static AtomicLong attempts = new AtomicLong(0); //count the number of combinations generated
  
  private static Object locker = new Object();
  
  private static long maxAttempts = 0; //total possible combinations of characters of specified lengths
  
  private static int maxLen = 0;
  
  private static long getMaxAttempts(int radix, int maxLen)
  {
    maxAttempts = (power(radix, maxLen) - 1)*radix /(radix-1);
    
    return maxAttempts;
  }
  
  //utility function to calculate powers of integers
  private static long power(int base, int exp)
  {
    if(exp < 0)
    {
      return 1/power(base, -exp);
    }
    else if(exp == 0)
    {
      return 1;
    }
    else{
      long pow = 1;
      for(int p = 1; p <= exp; p++)
      {
        pow*=base;
      }
      
      return pow;
    }
  }
  
  //the main work horse of this program, breaking all possible numbers into combinations
  private static void resolveRadix(int len, long num)
  {
    long[] retVal = new long[len];
    
    int pow = 0;
    int i = -1;

    int radix = len;
    
    for(i = 0; power(radix ,i ) <= num; i++ );
    
    for(int j = 0; j < len - i; j++)
    {
      retVal[j] = 0;
    }
    
    for(int k = len - i; k < len; k++)
    {
      long t = power(radix, i - 1);
      if(i > 1)
      {
      
        retVal[k] = (long)((num - (num % t)) / t);
      
      }
      else
      {
        retVal[k] = (num % radix);
      }
      num -= (retVal[k] * t);
      
      i--;
    }
    
    char[] combo = new char[len];
    
    for(int j = 0; j < len; j++)
    {
      combo[j] = dict[(int)retVal[j]];
    }
    
    String str = new String(combo);
    
    final long attemptsVal = attempts.incrementAndGet();
    
    attempts.set(attemptsVal);
  }
  
  private void generate()
  {
    for(int length = 1; length <= maxLen; length++)
    {
      int radix = dict.length;
      
      long max = (long)power(radix, length);

      for(int i=0;i<max;i++)
      {
        resolveRadix(radix, i);
      }
    }
    
  }
  
  public void run()
  {
    generate();
    
    synchronized(locker)
    {
      locker.notify();
    }
      
    ex.shutdownNow();
    
  }
  
  public static void main(String[] args)
  {
    
    ex = Executors.newSingleThreadExecutor();
    
    maxLen = 6;
    
    long atts = getMaxAttempts(dict.length, maxLen);
    
    StringGenerator threads = new StringGenerator();
    
    long start = System.currentTimeMillis();  //execution start time
    
    ex.execute(threads); //execute code parallelly
    
    try{
        
      synchronized(locker)
      {
        locker.wait();
      }
    }
    catch(InterruptedException ie)
    {
      ie.printStackTrace();
    }
    
    long attemptsVal = attempts.get(); //final total number of attempts
    
    long end = System.currentTimeMillis(); //execution end time
    
    double speed = (double)((1000 * attemptsVal)/(end - start)); //rate of generating combos
    
    double seconds = (double)(end - start) / 1000;
    
    System.out.println("per sec = "+speed);
    
    System.out.println("sec = "+seconds);
    
    System.out.println("words = "+attemptsVal);
    
    System.out.println("max words = "+atts);
    
  }
}

Execution after compilation is shown below:

Algorithm Generating String Combinations of Characters

In this post, I shall reveal another algorithm to generate all possible combinations of a given set of characters,of any predetermined range of lengths. For example, if we take a,b,c as possible characters in our combinations, and 1 to 3 as the range of lengths, then we have the following output:

a
b
c
aa
ab
ac
ba
bb
bc
ca
cb
cc
aaa
aab
aac
aba
abb
abc
....
ccc

This algorithm merely generates the combinations as strings of characters. It is upto the user of this algorithm to decide what to do with the generated string. I take no responsibility for what a user might actually do with this algorithm.

It is a non-recursive algorithm and is highly efficient in terms of usage of memory. Being non-recursive, it avoids the pitfall of call stack overflow, even with a large input space.

As with my other algorithm similar to this one here, one needs to implement parallelized code to max out CPUs and achieve a very high number of iterations per second.

The only limitation is that the combinations generated have a large amount of repetition of characters, which is exacerbated when the specified range of lengths is high.

The algorithm is as follows:

1. take length of string from minLen to maxLen, 
   array of characters being considered as dictionary
2. take current length of string as len
3. take radix as length of character dictionary
4. take max as radix to the power of len
5. from num = 0 to num = max - 1, resolve radix len, num
6. resolve radix as follows
   a. take retVal as array
   b. find p = highest power of radix <= num
   c. from j = 0 to len - p - 1, retVal[j] = 0
   d. from k = len - p to len - 1,
      i. t = radix to the power p - 1
      ii. if p > 1, retVal[k] = (num - (num % t)) / t;
          else retVal[k] = (num % radix)
      iii. num -= (retVal[k] * t)
      iv. p--
   e. build string from retVal using 
      str = empty string
      foreach(retVal as r)
          concat (dictionary[r]) with str
   f. do something with str
7. if len = maxLen 
      quit
   else
      increment len by 1 and goto step 2

The cornerstone of this algorithm is the resolve radix subroutine which does the main work in it. It works similar to conversion of decimal numbers to binary numbers. However, the difference is that in each of the bits, instead of just 0 and 1, we can put numbers ranging from 0 to length of the set of possible characters minus one.

In our case, the character set is a,b,c. So the numbers fitting in the bits are 0,1 and 2,with 0 mapping to ‘a’, 1 mapping to ‘b’ and 2 mapping to ‘c’. The total size generated is equal to the current length. So in our example above, there will be three main iterations, with the total bit size of the ‘number’ ranging from 1 to 3.

So the bit combinations range from

0
1
2
00
01
02
10
11
12
20
21
22
000
001
002
….
222

Using our mapping rules above, we get a from 0, b from 1, c from 2, aa from 00, ab from 01, ac from 02, etc.

Let this be a Valentine’s Day gift for everyone!

Sample Code for Algorithm to Create Combinations of Characters

In my post here, I described an algorithm to create all possible combinations from a set of characters. However, it allows repetitions of characters in the generated combinations. e.g aas, aaa and so on.
In this post, I will demonstrate an implementation of this algorithm in PHP, without any parallelization of any kind. I don’t know if it’s even possible to parallelize code in PHP.

You can run this code on LAMPP, WAMP, MAMP or XAMPP if you like. Successive trials of code execution may be faster than previous ones. Maybe, you all won’t like this code since it uses the “goto” keyword which is believed to lead to the creation of spaghetti code.  However, this was the easiest way to implement the algo for me.

<?php 

$dictionary = array('a', 'b', 'c', 'd', 'e');

$startLen = 1;
$stopLen = 4;

$currLen = 1;

//function to create string combination from array of indices
function getStringFromChars($indices)
{
  global $dictionary;
  $str='';

  for($j = 0; $j < count($indices); $j++)
  {
    $str.=$dictionary[$indices[$j]];
  }
  
  return $str;
}

//check condition to stop generating combos
function timeToStop($indices)
{
  
  global $dictionary;
  
  $stop = false;
  
  for($j = 0; $j < count($indices); $j++)
  {
    if($indices[$j] < count($dictionary) - 1)
    {
      return $stop;
    }
  }

  $stop = true;
  
  return $stop;
}

//main function
function generate($startLen, $stopLen)
{
  global $dictionary;
  $attempts = 0;
  
  for($currLen = $startLen; $currLen <= $stopLen; $currLen++)
  {
    step3:
    $chars = array();
    
    $indices = array();
    
    //init the arrays
    for($i = 0; $i < $currLen; $i++ )
    {
      $indices[$i] = 0;
      
      $chars[$i] = $dictionary[$indices[$i]];
    }
    
    step4:
    $working_index = $currLen - 1;
    
    step5:
    $str = getStringFromChars($indices);
    
    step6:
    echo $str;
    echo "<br />";
    $attempts++;
    
    if(timeToStop($indices))
    {
      if($currLen < $stopLen)
      {
        
        continue;
      }
      else
      {
        break;
      }
    }
    
    if($indices[$working_index] < count($dictionary) - 1)
    {
      $indices[$working_index]++;
      goto step5;
    }
    else
    {	
      if($currLen > 1)
      {

      
        while($indices[$working_index] == count($dictionary) - 1)
          $working_index--;
          
        if($working_index == -1)
        {
          if($currLen < $stopLen)
          {
            
            continue;
          }
          else
            break;
        }
        else
        {				
          $indices[$working_index]++;
          //set all indices to the right of working_index to 0
          
          for($k = $working_index + 1; $k < count($indices); $k++)
          {
            $indices[$k] = 0;
          }
          
          goto step4;
        }	
      }
      else
      {
      
        if($currLen < $stopLen)
        {
          
          continue;
        }
        else
          break;
      }
    }
    
  }

  return $attempts;
}

$start = microtime(true);

$atts = generate($startLen, $stopLen);

$end = microtime(true);

$time_taken = $end - $start;

$rate = $atts / $time_taken;

echo "Time(seconds): ".$time_taken;
echo "<br />";

echo "Attempts: ".$atts;
echo "<br />";

echo "Rate: ".$rate." iterations per second";

 

Algorithm to create all combinations from a set of characters

In this post, I shall reveal an algorithm that generates all possible combinations of a given set of characters of a specified range of lengths. The algorithm is as follows:

1.  take dict as a character array of possible characters in your string combinations
take currLen as integer, startLen as integer, stopLen as integer, chars as character array,  indices as integer array

2.  initialize currLen = startLen

3.  Set length of chars array to currLen, length of indices array to currLen

4.  set working_index  = currLen - 1

5.  get string from chars array as follows

i.  set i'th element of chars array to indices[i]'th element of dict

ii. Do the operation in the previous step (i) from i = 0 to i = currLen - 1

iii. concatenate the elements of chars array to generate a string combination of characters

6.  print string in step 5

7.  if all elements of indices equal length of dict - 1

         if currLen < stopLen

              increment currLen by 1

              go to step 3

         else

              quit

8.  if element of indices at position = working_index < length of dict - 1

        increment element of indices at position = working_index by 1

        go to Step 5

    else

        if currLen > 1

             decrement working_index by 1 till element of

             indices at position = working_index equals length of dict - 1

             if working_index equals -1

                 if currLen < stopLen

                     increment currLen by 1

                     go to Step 3

                 else

                     quit

              else

                  increment element of indices at position = working_index by 1

                  set all elements of indices to the right of position = working_index to 0

                  go to Step 4

        else

            if currLen < stopLen

               increment currLen by 1

               go to Step 3

            else

               quit

 

At first glance, this algorithm may look like a brute force algorithm, but I seriously doubt that it can be used to do naughty things like cracking passwords. Of course, to unleash the full power of this algorithm, one needs to parallelize the code in his implementation of this algorithm. That way we can max out the cpu cores and enjoy a very large number of iterations per second.

It may, however, be used to create a reverse lookup database of one way cryptographic hash functions. But, with the use of salts being common nowadays, such a database of all possible plaintexts and their hashes may not be useful after all.

The best part about this algorithm is that it is non-recursive and so avoids an inordinately large number of function calls and a potential call stack overflow. This is true especially when the dictionary of characters is very large.

So, all in all, this algorithm may be used as a fun academic exercise. Or, perhaps one of you guys may come up with a practical use for this algorithm.